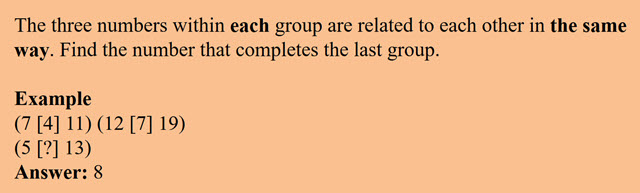Online Tests & Practice Sample Papers for 11 Plus Verbal Reasoning
Visuteach sells GL Assessment style interactive online 11 plus verbal reasoning tests and 24 verbal reasoning (VR) papers. These help prepare for GL Assessment 11 plus verbal reasoning entrance exams and admissions assessments for independent, private and grammar schools.
Visuteach papers and online software tests cover all 21 types of GL Assessment verbal reasoning question. Examples of the 21 types of question are shown further down this web page. Our papers 1 to 12 are drawn from our question types 1 to 15, and our papers 13 to 24 are drawn from all 21 question types.
Our 11 plus VR membership package contains all of Visuteach’s 24 verbal reasoning papers and 24 online software test versions of the 24 papers. Visuteach’s online verbal reasoning package contains a total of 1,920 multiple-choice VR questions which are presented as 24 complete VR tests (with 80 questions per test, to be completed in 50 minutes) as well as 96 shorter tests (with 20 questions per test, to be completed in 12.5 minutes). The short twenty question tests are ideal for daily practice because they require less time to be set aside for learning and because they can be completed quickly. Our tests are online multiple-choice tests with automatic and immediate marking.
In addition, in our 11 plus VR software membership package, Visuteach breaks down all of our 1,920 verbal reasoning questions by type i.e. we group all of the questions into the 21 types of GL Assessment verbal reasoning questions. This allows students to concentrate and focus on the question types that they find most difficult rather than spending time on mixed and easier question types.
Visuteach’s verbal reasoning questions are similar to, and based upon, the questions in the official GL Assessment familiarisation practice paper packs which are sold online and in shops.
This page contains a demo of our paper tests and a computer software demo of our online 11+ (11 plus) GL Assessment verbal reasoning (VR) tests for grammar, independent, private and secondary school entrance exams.
Video Explanations For Difficult Question Types
Visuteach has 1,920 verbal reasoning questions covering the 21 types of VR questions. We have detailed explanations, written into our software tests, on how to solve 417 of these questions. The explanations are for the difficult question types i.e.
- type 1 – crack the letter code
- type 2 – complete the letter series
- type 3 – complete the letter sentence
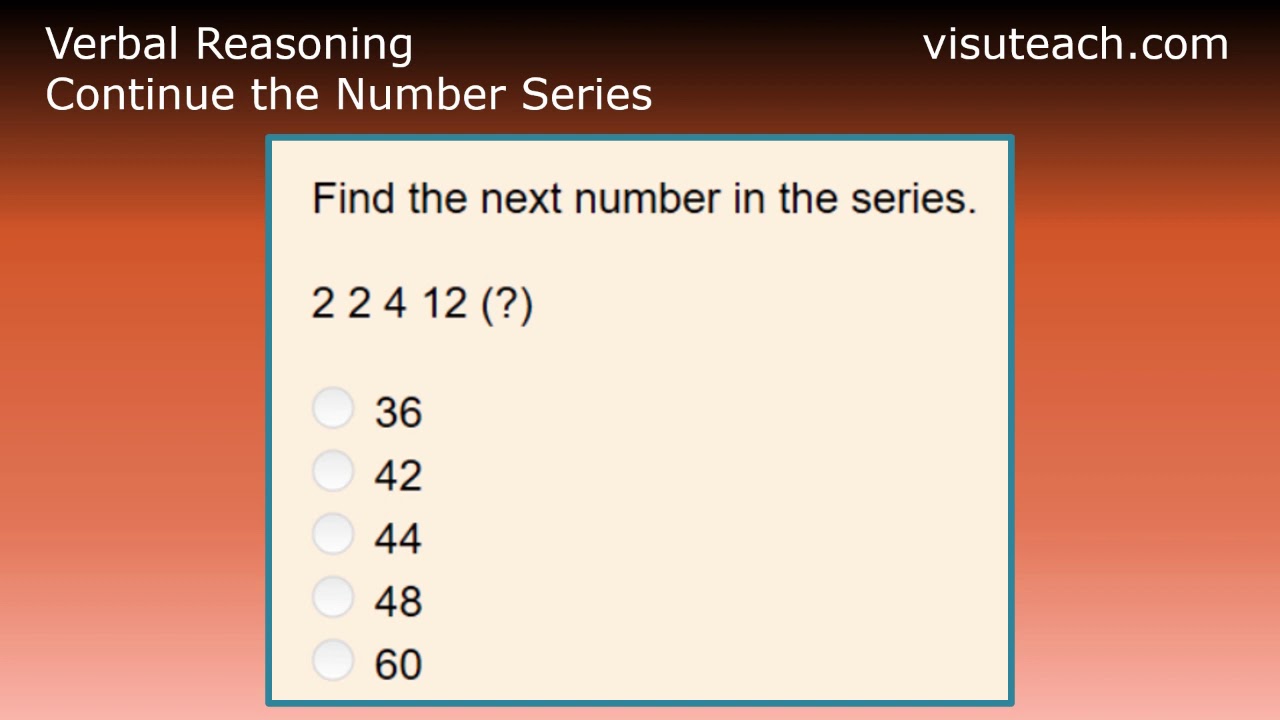
- type 10 – continue the number series
- type 15 – explore the facts & solve the riddle
- type 18 – find the missing number
- type 19 – crack the number code
The remaining question types do not require detailed explanations because the answers are generally self-explanatory. However, if you need any help on any question type, contact us by email and we will provide an explanation.
Below, we have video samples of some of our explanations.
11 Plus Verbal Reasoning (VR) Paper Demo
Download and print out the answer sheet for the question paper by clicking on the link below:
The 11 plus question paper and the answers shown below can be displayed in full screen mode by clicking on the Full Screen icon (which has has four small white diagonal arrows) on the toolbar at the bottom of the paper or the bottom of the answers. To exit from full screen mode, you can click on the Full Screen icon or press the Esc key on your keyboard.
To scroll the paper, you can either use the scroll bars to the right and bottom of the paper, or you can use the up and down arrow icons on the toolbar, or you can just hover anywhere within the paper until you see the hand icon and then just drag the hand up or down.
For mobile users, you can use pinch and zoom to enlarge the text and use your finger to scroll.
Note that when you buy a paper, you cannot print out the paper and the answers shown below. You can only view them online for a period of 1 year.
Question Paper
Answers
11 Plus Verbal Reasoning Software Demo Tests
The verbal reasoning demo test below shows the 21 types of question (with answers immediately after each question).
11 Plus Verbal Reasoning Demo Test 1
The 11 plus demo below is a short 20 question, 12.5 minute timed test (with answers at the end of the test).
11 Plus Verbal Reasoning Demo Test 2
The following VR demo tests are short untimed tests (with answers immediately after each question).
11 Plus Verbal Reasoning Demo Test 3
The 21 GL Assessment Verbal Reasoning Question Types
There are 21 question types that can appear in GL Assessment 11 plus verbal reasoning exams. (Note that these 21 types can also be considered to be 22 types, since one of the types contains two distinct question types i.e. the two types Explore the Facts and Solve the Riddle.)
The official GL Assessment Sample Pack 1 (which can be bought in shops and online) contains four 50 question tests covering Visuteach’s question types 1 to 15, and the official GL Assessment Sample Pack 2 contains four 50 question tests covering Visuteach’s question types 1 to 15 and some questions from Visuteach’s question types 16 to 21.
Visuteach’s GL Assessment 11 plus verbal reasoning membership package contains a total of twenty-four 50 question tests. Questions in tests 1 to 12 are similar to the questions in the 4 tests of the official GL Assessment Sample Pack 1 (i.e. they cover Visuteach question types 1 to 15) and questions in tests 13 to 24 are similar to the questions in the 4 tests of the official GL Assessment Sample Pack 2 (i.e. they cover Visuteach question types 1 to 15 as well as types 16-21).
In addition, Visuteach’s GL Assessment 11 plus verbal reasoning membership package organises and presents all of our 1,920 verbal reasoning questions by each of the 21 question types. This allows the user to focus on particular question types which present the most difficulty rather than having to take full tests which combine questions from a a number of different types.
Visuteach’s classification of the 21 GL Assessment verbal reasoning question types (along with examples) is given below: