Online GL Assessment 11 Plus Maths Tests & Sample Practice Papers
Visuteach provides GL Assessment style 11 plus online software tests which help prepare for GL Assessment secondary transfer 11 plus maths entrance exams and selective admissions tests for independent, private and grammar schools.
Visuteach’s interactive software membership package contains ten 11 plus GL Assessment style online maths papers and the same questions in ten online software tests. There are 500 multiple-choice maths questions, with answers and explanations for each question, which are presented as 10 complete maths tests (with 50 multiple-choice questions per test, to be completed in 50 minutes) as well as 50 shorter tests (with 10 multiple-choice questions per test, to be completed in 10 minutes). The short ten question tests are ideal for daily practice since they require less time to complete.
Video Explanations of Some GL Assessment Style Maths Questions
GL Assessment Maths 11 Plus Software Test Demos
Visuteach Online GL Assessment 11 Plus Maths Membership Package
The following two 11 plus demo tests are untimed 10 question tests with answers immediately after each question.
GL Assessment 11 Plus Maths Untimed Demo Test 1
GL Assessment 11 Plus Maths Untimed Demo Test 2
The following two GL Assessment demo tests are timed 10 question tests with answers at the end of the test.
You can download and print out a pdf file of the questions in Visuteach’s 11 plus maths software demos by clicking on the link below:
Visuteach GL Assessment 11 Plus Maths Sample Questions
The questions, answers and explanations are shown in the tabs below.
Jack was x years old 4 years ago. How old will he be 6 years from now?
Choose one of the following answers:
x+2
x+4
x+6
x+10
x+8
Answer: x+10
Jack was x years old 4 years ago, so he is now x+4 years old. In 6 years’ time he will be 6 years older i.e. he will be x+4+6 = x+10 years old
A, B and C are the angles of an isosceles triangle. Angle A measures 70°. Angle B is greater than 60°. What is the size of angle C?
Choose one of the following answers:
70°
50°
60°
55°
40°
Answer: 40°
An isosceles triangle has at least 2 equal sides and 2 equal angles. We also know that the angles inside a triangle add up to 180°.
Angle A is 70°, angle B is greater than 60° and therefore angle C is less than 50°. We know that two of these angles must be equal in order for this triangle to be isosceles and the only way that this can be is if angle B = angle A i.e. angle B = 70°. Therefore angle C = 40°
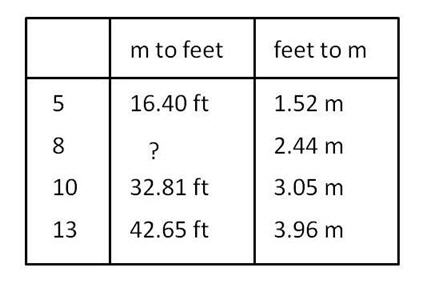
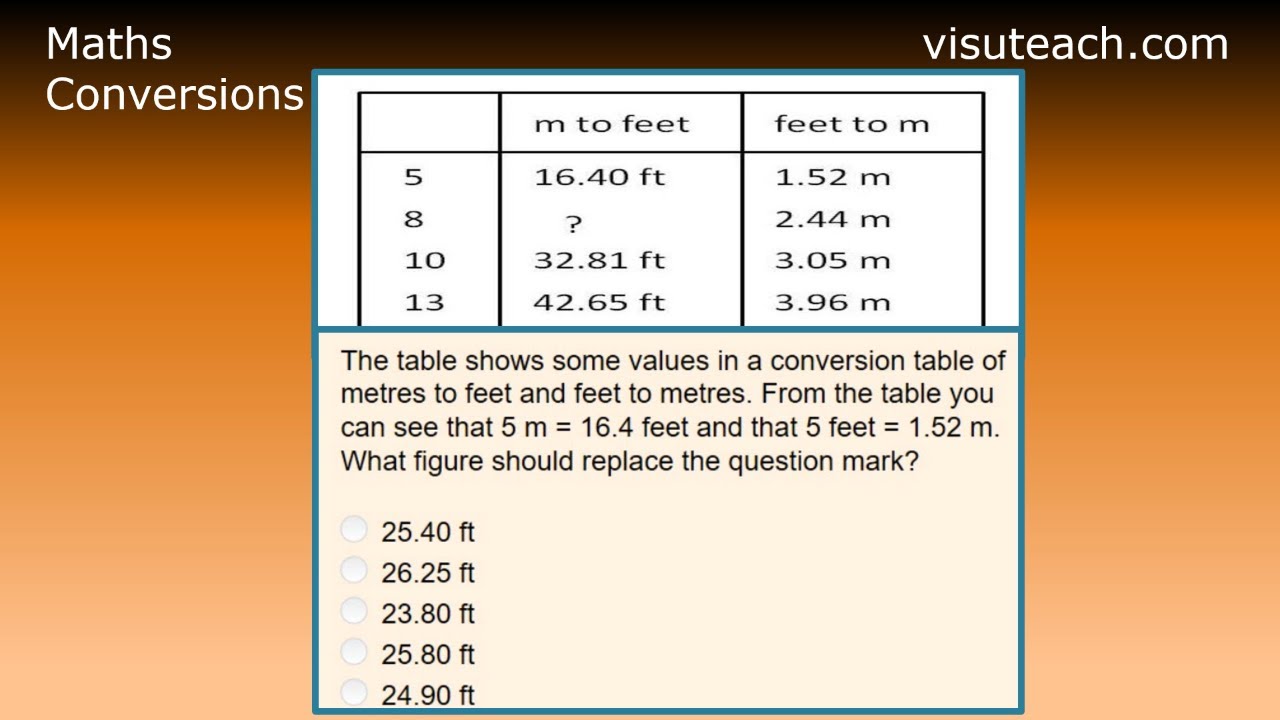
The table shows some values in a conversion table of metres to feet and feet to metres. From the table you can see that 5 m = 16.4 feet and that 5 feet = 1.52 m. What figure should replace the question mark?
Choose one of the following answers:
25.40 ft
26.25 ft
23.80 ft
25.80 ft
24.90 ft
Answer: 26.25 ft
The ? represents the value of 8 metres in feet. In the table we are given the values of 5 m, 10 m and 13 m in feet, and we can use this information to find the value of 8 m in feet. We do this by seeing that 8 = 13 – 5 and therefore the value of 8 m in feet will be the value of 13 m in feet minus the value of 5 m in feet = 42.65 – 16.40 = 26.25 feet (i.e. 26.25 ft)
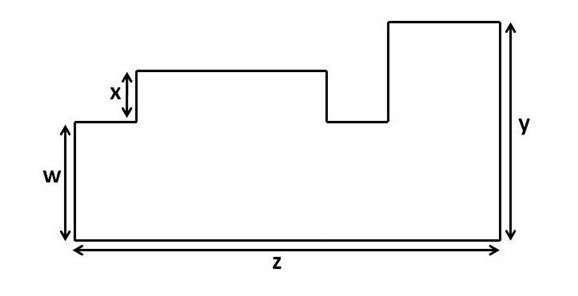
What is the perimeter of this shape?
Choose one of the following answers:
2x+2y+2z
w+2x+2z
y+w+x+2z
2w+y+2z
y+w+x+z
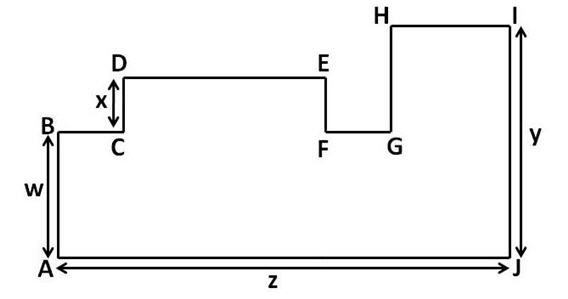
the perimeter of this shape is the sum of the lengths of the horizontal segments and the vertical segments
the sum of the lengths of the horizontal segments = AJ+BC+DE+FG+HI
BC+DE+FG+HI is the same as the length of AJ (i.e. z), so
the sum of the lengths of the horizontal segments = AJ+(BC+DE+FG+HI) = z+z = 2z
the sum of the lengths of the vertical segments = JI+AB+CD+FE+GH
AB+GH is the same length as JI (i.e. y), so
the sum of the lengths of the vertical segments = JI+AB+CD+FE+GH = JI + (AB+GH) +CD+FE = y+y+CD+FE = 2y+CD+FE
CD is of length x and CD is the same length as FE, so we have
the sum of the lengths of the vertical segments = 2y+CD+FE = 2y+x+x = 2y+2x
so the perimeter of the shape = sum of the lengths of the horizontal segments + sum of the lengths of the vertical segments = 2z+2y+2x = 2x+2y+2z
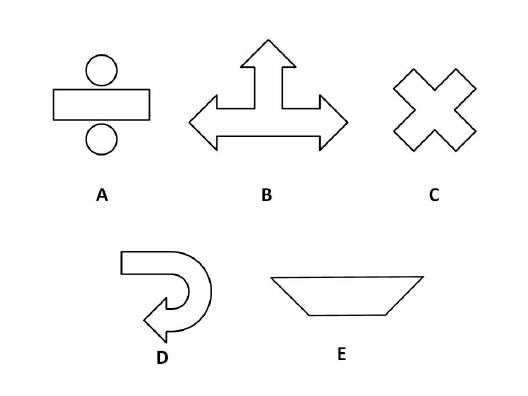
Which of these shapes have rotational symmetry?
Choose one of the following answers:
A and B
B and E
C and D
A and C
C and E
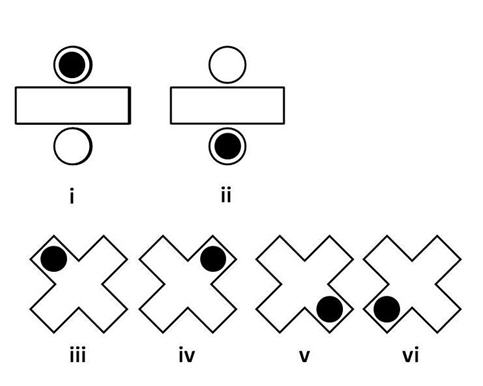
shape A has rotational symmetry of order 2 (i.e. it fits onto itself twice as it is turned through 360°). This can be seen in (i) and (ii) above. We have put a blob on the shape in order to more easily see what happens when we rotate the shape. We start from position (i) and end up at position (ii) after rotating the shape 180° clockwise. From position (ii) we end up back at position (i) by rotating the shape a further 180° clockwise. So there are 2 positions in which the shape looks the same when being rotated through 360° and therefore shape A has rotational symmetry of order 2.
shape C has rotational symmetry of order 4 (i.e. it fits onto itself four times as it is turned through 360°). This can be seen in (iii), (iv), (v) and (vi) above. We have put a blob on the shape in order to more easily see what happens when we rotate the shape. We start from position (iii) and end up at position (iv) after rotating the shape 90° clockwise. From position (iv) we end up at position (v) after rotating the shape 90° clockwise. From position (v) we end up at position (vi) after rotating the shape 90° clockwise. From position (vi) we end up back at position (iii) after rotating the shape a further 90° clockwise. So there are 4 positions in which the shape looks the same when being rotated through 360° and therefore shape C has rotational symmetry of order 4.
If 5x – 6 = 7x + 4, what is x?
Choose one of the following answers:
3
-3
-5
5
Answer: -5
5x-6 = 7x+4
to solve for x you need to isolate all of the x terms on one side of the equation. Performing the same operation on both sides of an equation leaves the equation unchanged (i.e. the equality still holds true). We use this fact to help us isolate x terms. First we subtract 5x from both sides of the equation i.e.
5x – 6 – 5x = 7x + 4 – 5x which gives us -6 = 2x + 4
then we subtract 4 from both sides of the equation and we get
– 6 – 4 = 2x + 4 – 4 i.e. -10 = 2x
then we divide both sides of the equation by 2 and we get
-5 = x i.e. x = -5
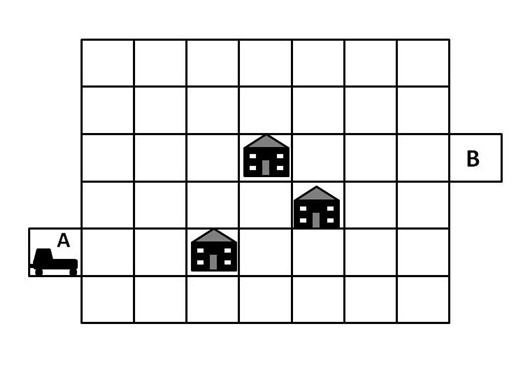
A radio controlled car needs to be guided along the white squares from point A to point B, avoiding the houses on the way. The car can only move FORWARD, TURN RIGHT 90° and TURN LEFT 90°.
Which instructions should you use to guide the car?
Choose one of A, B, C or D
A) FORWARD 2, TURN RIGHT 90°,
FORWARD 1, TURN LEFT 90°,
FORWARD 4, TURN LEFT 90°,
FORWARD 4, TURN RIGHT 90°,
FORWARD 2
B) FORWARD 2, TURN LEFT 90°,
FORWARD 1, TURN RIGHT 90°,
FORWARD 4, TURN LEFT 90°,
FORWARD 1, TURN RIGHT 90°,
FORWARD 2
C) FORWARD 2, TURN RIGHT 90°,
FORWARD 1, TURN LEFT 90°,
FORWARD 3, TURN LEFT 90°,
FORWARD 3, TURN RIGHT 90°,
FORWARD 3
D) FORWARD 2, TURN RIGHT 90°,
FORWARD 1, TURN LEFT 90°,
FORWARD 4, TURN LEFT 90°,
FORWARD 3, TURN RIGHT 90°,
FORWARD 2
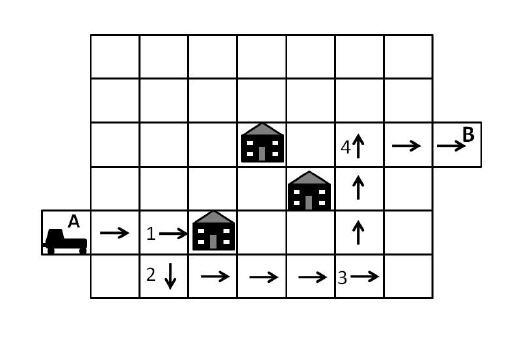
The car moves forward 2, so it moves from position A to position 1. The car is then facing towards the east as shown by the arrow in the square at position 1. The car then turns right 90° (i.e. it turns 90° in a clockwise direction), so it is now facing south. It then moves forward 1 and ends up in position 2. The car then turns left 90° (i.e. it turns 90° in an anti-clockwise direction), so it is now facing east. The car then moves forward 4 so it ends up at position 3. The car then turns left 90° (i.e. it turns 90° in an anti-clockwise direction), so it is now facing north. The car then moves forward 3 so it ends up at position 4. The car then turns right 90° (i.e. it turns 90° in a clockwise direction), so it is now facing east. The car then moves forward 2 so it ends up at position B.
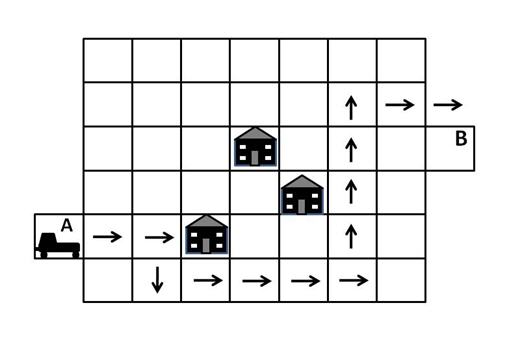
Answer A is incorrect, because the car does not end up at position B, as shown in the diagram below:
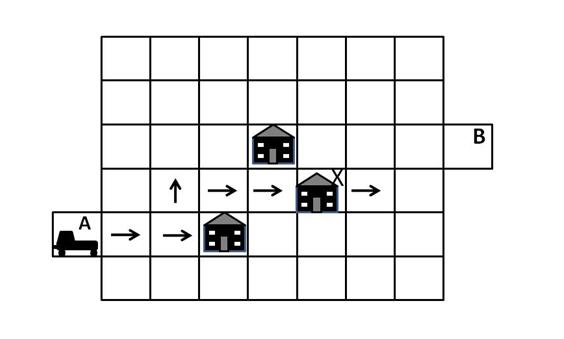
Answer B is incorrect, because the car crashes into the house at position X, as shown in the following diagram:
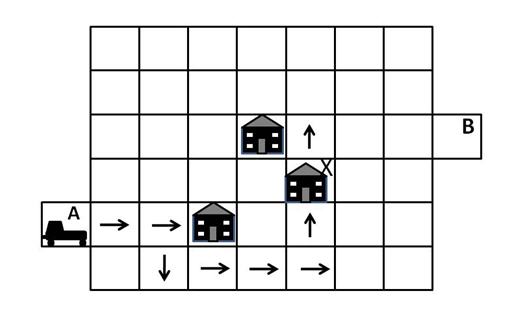
Answer C is incorrect, because the car crashes into the house at position X, as shown in the diagram below:
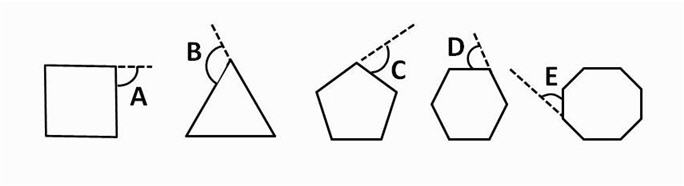
The diagram shows exterior angles for 5 regular polygons. Which one of these angles is the smallest?
Choose one of A, B, C, D or E
Answer: E
There are a number of ways of working this question out. Two ways are as follows :
a) for a regular polygon, all of its sides are equal in length and all of its interior angles are equal. Each exterior angle of the polygon has a corresponding interior angle and the exterior angle = 180° – interior angle. Therefore the larger the interior angle of the polygon is, then the smaller the exterior angle is. By looking at the polygons in the question, we can see that the more sides the polygon has, the greater is each interior angle and therefore the smaller is each exterior angle. Therefore the polygon with the greatest number of sides has the smallest exterior angle. The octagon has the most sides and therefore the answer is E (i.e. angle E)
b) the sum of the exterior angles of any polygon is 360°. A polygon with n sides has n interior angles and n corresponding exterior angles. For a regular polygon, all of its interior angles are equal to each other and also its exterior angles are equal to each other. For a regular polygon with n sides, each of its n exterior angles is equal and the sum of its n exterior angles is 360°, so each exterior angle will be equal to 360°/n. Therefore the larger the value of n, the smaller the value of the exterior angle (e.g. if n = 3 then each exterior angle will be 360/3 = 120° and if n = 6 then each exterior angle will be 360/6 = 60°). So the regular polygon with the greatest number of sides will be the one that has the smallest exterior angle. The octagon has the most sides and therefore the answer is E (i.e. angle E).
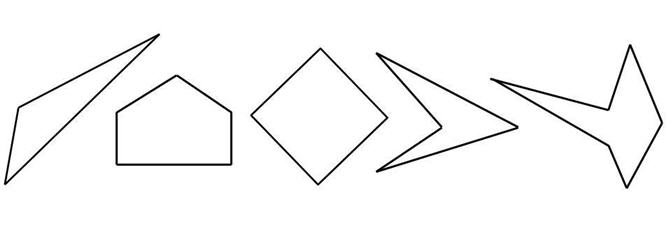
How many of these shapes contain interior reflex angles?
Choose one of the following answers:
1
2
3
4
5
a reflex angle is an angle between 180° and 360°. The interior reflex angles of the shapes in the question are shown below
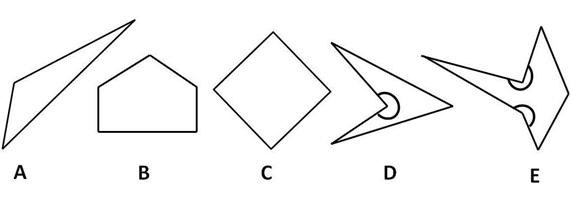
so there are two shapes which contain interior reflex angles i.e. shapes D and E. So the answer is 2
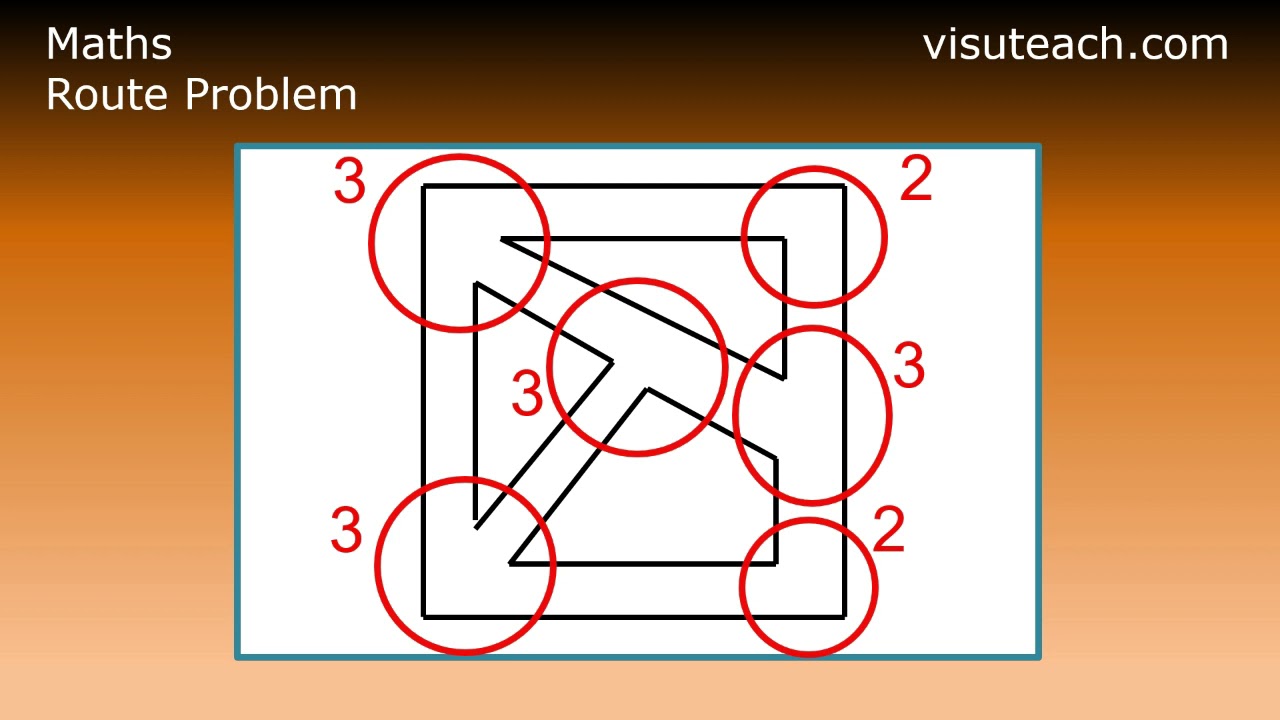
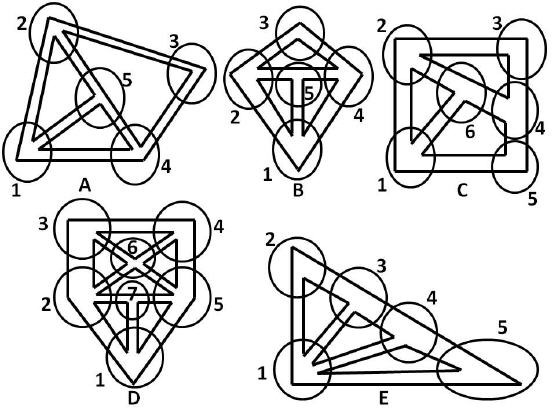
A milkman delivers milk to certain housing estates. The street layout of the housing estates is shown in the diagram above. The milkman wants to avoid visiting the same street more than once, but there are no restrictions on him passing over the same street corners. On which housing estate is this possible?
Choose one of A, B, C, D or E
Answer: E
You can solve this problem by trying to trace a path through the streets of each housing estate and finding the housing estate that allows the milkman to visit each street once only. However, there is a quicker, easier way to work the problem out.
We will first define a vertex as being a point at which paths (i.e. streets in this example) meet. The degree of the vertex is the number of paths that meet at the vertex. The degree of a vertex is odd if there are an odd number of paths meeting at the vertex, and is even if there are an even number of paths meeting at the vertex.
Looking at the housing estates in the question, we can draw rings around the vertices of each housing estate. Doing this we get the following diagram
The key facts you need to know to solve this problem are :
If there are fewer than 3 vertices of odd degree then there is a path around the housing estate which allows the milkman to visit each street once only.
If there are more than two vertices of odd degree then there is no path around the housing estate which allows the milkman to visit each street once only.
So the solution can be found by eliminating any housing estate that has more than 2 vertices of odd degree, and looking for the housing estate that has fewer than 3 vertices of odd degree.
A is incorrect because housing estate A has 4 vertices of degree 3 (i.e. vertices 1, 2, 4 and 5) and 1 vertex of degree 2 (i.e. vertex 3). Therefore it has 4 vertices of odd degree and 1 vertex of even degree. It has more than two vertices of odd degree and is therefore not the correct answer.
B is incorrect because housing estate B has 4 vertices of degree 3 (i.e. vertices 1, 2, 4 and 5) and 1 vertex of degree 2 (i.e. vertex 3). Therefore it has 4 vertices of odd degree and 1 vertex of even degree. It has more than two vertices of odd degree and is therefore not the correct answer.
C is incorrect because housing estate C has 4 vertices of degree 3 (i.e. vertices 1,2,4 and 6) and 2 vertices of degree 2 (i.e. vertices 3 and 5). Therefore it has 4 vertices of odd degree and 2 vertices of even degree. It has more than two vertices of odd degree and is therefore not the correct answer.
D is incorrect because housing estate D has 4 vertices of degree 3 (i.e. vertices 1, 3, 4 and 7) and 3 vertices of degree 4 (i.e. vertices 2, 5 and 6). Therefore it has 4 vertices of odd degree and 3 vertices of even degree. It has more than two vertices of odd degree and is therefore not the correct answer.
E is correct because housing estate E has 2 vertices of degree 3 (i.e. vertices 3 and 4), 2 vertices of degree 2 (i.e. vertices 2 and 5) and 1 vertex of degree 4 (i.e. vertex 1). Therefore it has 2 vertices of odd degree and 3 vertices of even degree. It has fewer than 3 vertices of odd degree and is therefore the correct answer.
In summary, to solve these problems quickly, all you need to do is to eliminate any housing estate that has more than 2 vertices of odd degree. The solution will be the housing estate that has fewer than 3 vertices of odd degree.
Note that a path (which covers every street without visiting a street more than once) around housing estate E can be found by starting at a vertex of odd degree. For example, we can start at vertex 3 (which has an odd degree of 3), and one correct path is:
vertex 3 to vertex 2, vertex 2 to vertex 1, vertex 1 to vertex 3, vertex 3 to vertex 4, vertex 4 to vertex 1, vertex 1 to vertex 5 and vertex 5 to vertex 4.
Carol has 23 photo albums, and each album contains 480 photos. How many photos does she have in total?
Choose one of the following answers:
12,160
10,840
11,120
12,060
11,040
Answer: 11,040
One photo album has 480 photos, so 23 photo albums will have 23 x 480 = 20×480 + 3×480 = (20×400 + 20×80) + (3×400 + 3×80) = 8000 + 1600 + 1200 + 240 = 11,040 photos
Anthony draws a plan of his house using a scale of 3 cm to 7 m. The kitchen has a length of 7.5 cm on the plan. What is the real length of the kitchen?
Choose one of the following answers:
17.5 m
18.2 m
17.4 m
18.5 m
19.4 m
Answer: 17.5 m
3 cm on the plan represents 7 real metres.
The kitchen has a length of 7.5 cm on the plan.
7.5 cm is 2.5 x 3 cm because 7.5/3 = 2.5
3 cm represents 7 real metres, so 7.5 cm = 2.5 x 3 cm and represents 2.5 x 7 m = 17.5 m
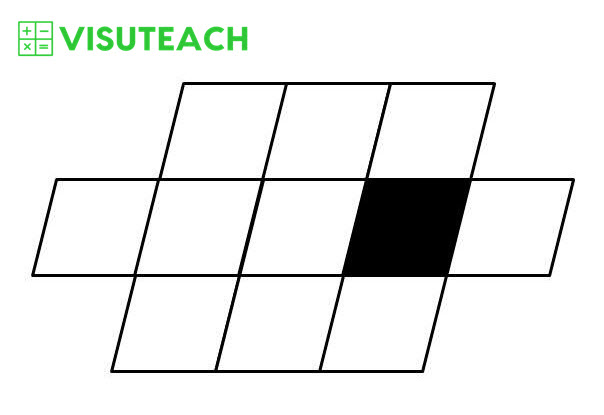
The area of the black parallelogram is 30 mm². What is the area of the large shape?
Choose one of the following answers:
2400 mm2
0.24 cm2
24,000 mm2
2.4 cm2
24 cm2
Answer: 2.4 cm²
The large shape is made up of 8 parallelograms of equal size. Each parallelogram has an area equal to the area of the black parallelogram (i.e. 30 mm²). So the total area of the shape is 8 x 30 mm² = 240 mm².
1 cm = 10 mm, 1 cm² = 1 cm x 1 cm = 10 mm x 10 mm = 100 mm²,
so 1 cm² = 100 mm²,
so 240 mm² = 2.4 x 100 mm² = 2.4 cm²
(3×5) + (3×2)
(2×3) + (2×5)
(5×2) + (5×3)
2 x (5+3)
3x5x2
For each type of ice cream, there are 5 types of sorbet. There are 3 types of ice cream and therefore there are 15 (i.e. 3×5) combinations of ice cream and sorbet. For each one of these 15 combinations of ice cream and sorbet, there are 2 types of tart. Therefore there are 30 (i.e. 3x5x2) combinations of ice cream, sorbet and tart.
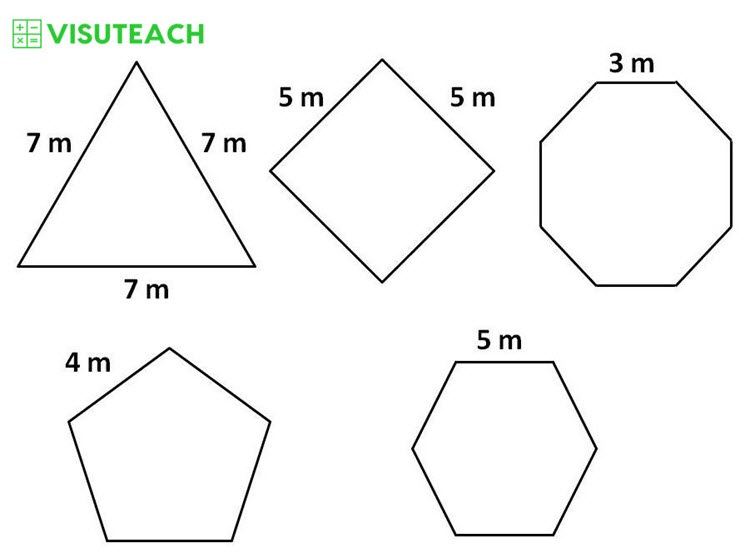
How many of these shapes have a perimeter greater than 20 metres?
Choose one of the following answers:
4
3
5
2
1
Perimeter of shape A is 7 m + 7 m + 7 m = 21 m
Perimeter of shape B is 5 m + 5 m + 5 m + 5m = 20 m
Perimeter of shape C is 3 m + 3 m + 3 m + 3 m + 3 m + 3 m + 3 m + 3 m = 24 m
Perimeter of shape D is 4 m + 4 m + 4 m + 4 m + 4 m = 20 m
Perimeter of shape E is 5 m + 5 m + 5 m + 5 m + 5 m + 5 m = 30 m
Shapes A, C and E have perimeters greater than 20 m. So there are 3 shapes that have perimeters greater than 20 m.
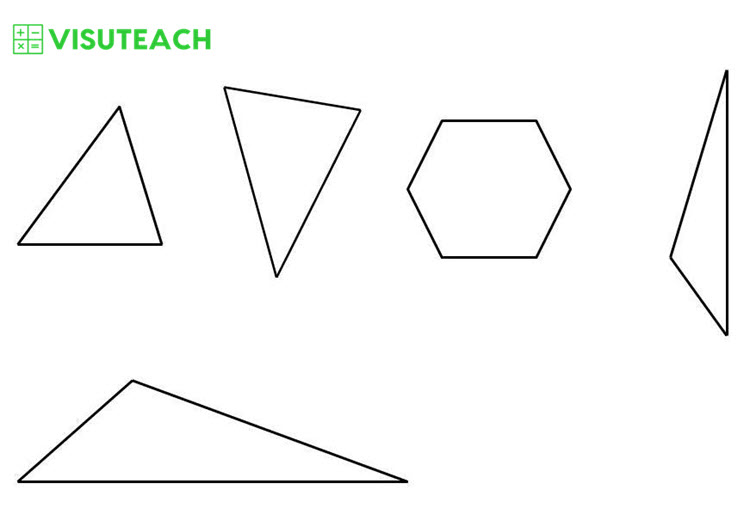
How many of these shapes contain obtuse angles?
Choose one of the following answers:
1
2
3
4
5
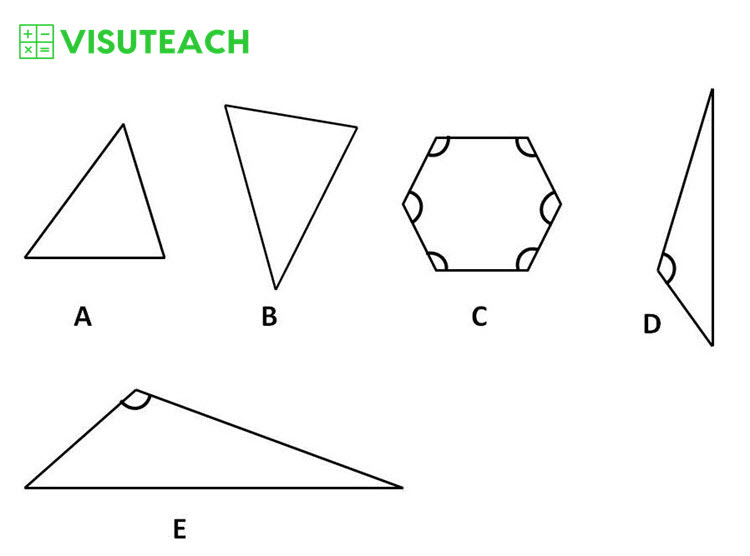
An obtuse angle is an angle greater than 90° and less than 180° (i.e. an angle between 90° and 180°)
Shapes, C, D and E contain obtuse angles, and these angles are marked in the diagram above. So there are 3 shapes that contain obtuse angles.
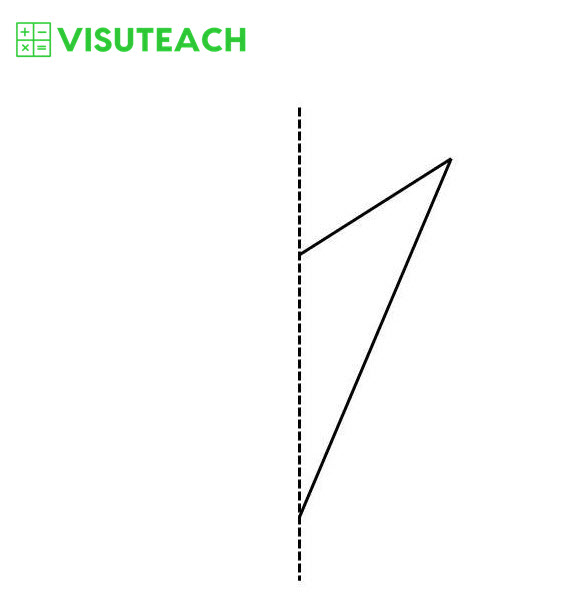
The diagram above shows part of a shape and its line of symmetry. What is the name of the complete shape?
Choose one of the following answers:
triangle
rectangle
pentagon
kite
rhombus
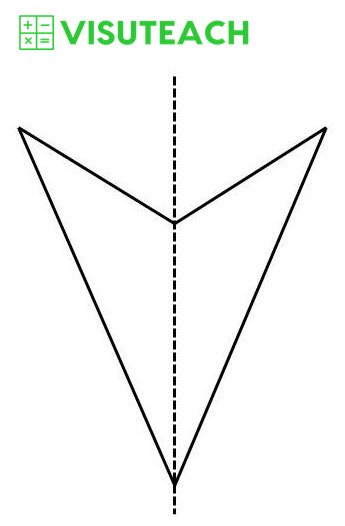
The complete shape is shown above and is called a kite.
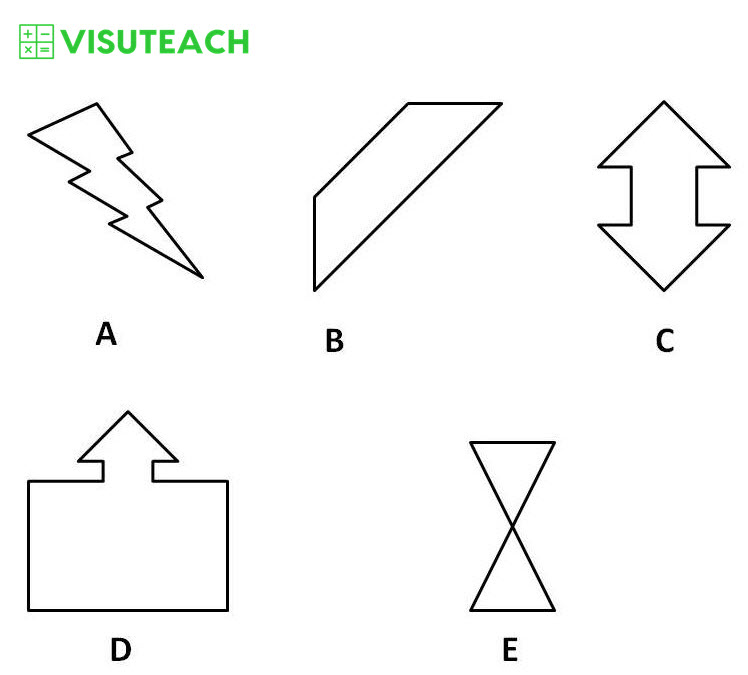
Which of these shapes have rotational symmetry?
Choose one of the following answers:
A and C
C and E
B and D
D and E
E and B
Answer: C and E
Shapes C and E have rotational symmetry of order 2 (i.e. they each fit onto themselves twice as they are turned through 360°). Each of these shapes fits onto itself when rotated by 180° and then fits onto itself again when rotated a further 180°. So there are 2 times in which each of these shapes looks the same when being rotated through 360° and therefore each of these shapes has rotational symmetry of order 2.
The other shapes do not have rotational symmetry.
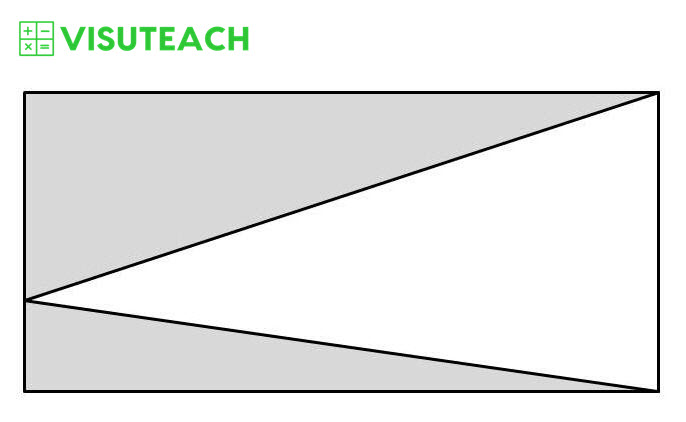
The area of the white triangle is 46 cm². What is the area of the shaded part of the rectangle?
Choose one of the following answers:
56 cm²
48 cm²
54 cm²
46 cm²
58 cm²
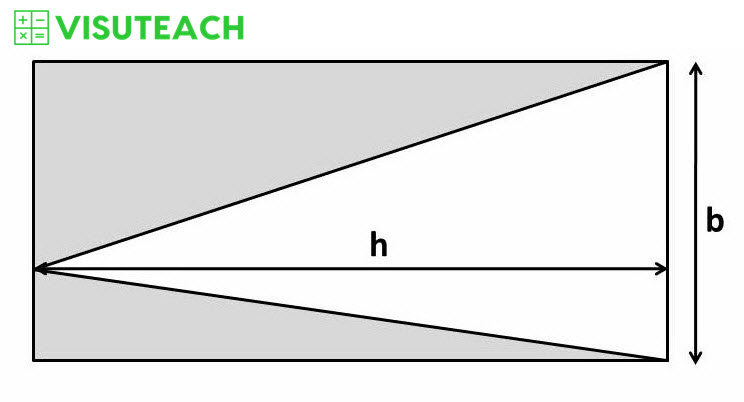
The area of the rectangle is bh and the area of the white triangle is ½ x base of the triangle x perpendicular height of the triangle (i.e. ½bh). So the area of the rectangle is twice the area of the white triangle.
Area of rectangle = shaded area + area of white triangle = 2 x area of white triangle
So the area of the shaded part of the rectangle must be equal to the area of the white triangle i.e. 46 cm²
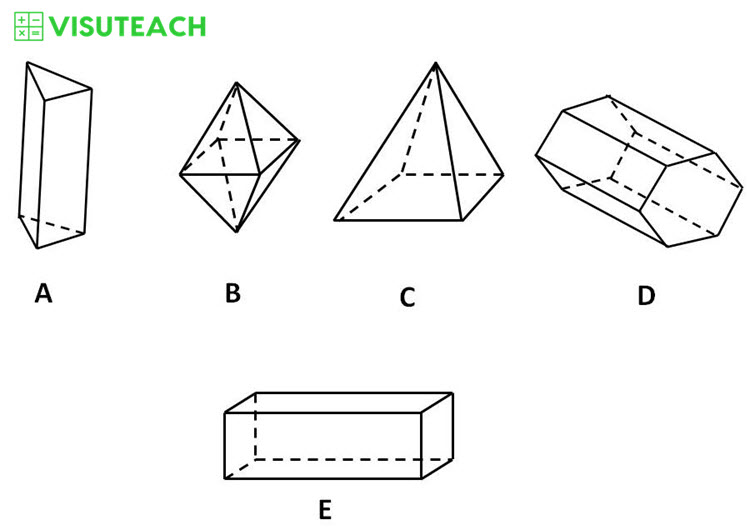
How many shapes have more vertices than faces?
Choose one of the following answers:
1
2
3
4
5
Answer: 3
Shape A has 6 vertices and 5 faces
Shape B has 6 vertices and 8 faces
Shape C has 5 vertices and 5 faces
Shape D has 12 vertices and 8 faces
Shape E has 8 vertices and 6 faces
So there are three shapes that have more vertices than faces i.e. shapes A, D and E